Γεωμετρικός αριθμός: μια άλλη «πλευρά» του Πλάτωνος (Χαράλαμπος Σπυρίδης, Καθηγητής Μουσικής Τμήματος Μουσικών Σπουδών της Φιλοσοφικής Σχολής του Παν/μίου Αθηνών)
3 Φεβρουαρίου 2017
 Τέλειον Μείζον Σύστημα κατά χρώμα παρά Πλάτωνι: Θα σας ομιλήσω περί του υπό του Πλάτωνος λεγομένου γεωμετρικού αριθμού. Η ασάφεια της αναφοράς του Πλάτωνος περί του γεωμετρικού αριθμού είναι τοσούτον μεγάλη, ώστε είχεν καταστεί παροιμιώδης για τους αρχαίους. Τούτου του γεγονότος ένεκα υπήρξεν προβληματισμός μήπως παλαιόθεν εγένετο λαθροχειρία επί του κειμένου.
Τέλειον Μείζον Σύστημα κατά χρώμα παρά Πλάτωνι: Θα σας ομιλήσω περί του υπό του Πλάτωνος λεγομένου γεωμετρικού αριθμού. Η ασάφεια της αναφοράς του Πλάτωνος περί του γεωμετρικού αριθμού είναι τοσούτον μεγάλη, ώστε είχεν καταστεί παροιμιώδης για τους αρχαίους. Τούτου του γεγονότος ένεκα υπήρξεν προβληματισμός μήπως παλαιόθεν εγένετο λαθροχειρία επί του κειμένου.
Το δυστύχημα για την Φιλοσοφίαν είναι ότι εις ουδέν εκ των σωζομένων φιλοσοφικών συγγραμμάτων δεν υπάρχει ίχνος διασαφηνίσεως περί του συγκεκριμένου προβλήματος.
Όντως, απαιτείται υψίστου βαθμού μύησις, ήτοι βαθύταται γνώσεις Πυθαγορείου Αριθμητικής, Γεωμετρίας και Μουσικής, αι οποίαι εις ολιγόλεπτον ομιλίαν δεν μεταφέρονται. Όμως, εντός του τακτού χρόνου θα παραθέσω την λύσιν του προβλήματος για πρώτην φοράν, το οποίον εν ολίγοις αφορά εις την κατατομήν του κανόνος κατά χρώμα παρά Πλάτωνι ή, όπως λέγομεν εις την Βυζαντινήν Μουσικήν, κατά το χρωματικόν γένος.
Ο Πλούταρχος εις το έργον του Περί Μουσικής εκθειάζει τον Πλάτωνα ως εμπειρότατον περί των θεμάτων της αρμονίας (=διαπασών) «ὁ Πλάτων … ἔμπειρος ἁρμονίας ἦν».
Εκκινούμεν εκ της σεμνής, ουρανίου φύσεως, θείας, καλής και δαιμονίου αρμονίας, το μουσικό διάστημα το οποίον εκθειάζει ο Αριστοτέλης «ὅτι σεμνή ἡ ἁρμονία καί θεῖόν τι καί μέγα, Ἀριστοτέλης ὁ Πλάτωνος ταυτί λέγει ἡ δέ ἁρμονία ἐστίν οὐρανία τήν φύσιν ἔχουσα θείαν καί καλήν καί δαιμονίαν».
Το διάστημα της αρμονίας (2:1), παρεμβάλλοντες εν πρώτοις εν αὐτῷ δύο μεσότητας, το καθιστώμεν τετραμερές. Αι δύο μεσότητες αύται είναι η τρίτη και η τετάρτη εκ των δέκα Πυθαγορείων μεσοτήτων, ήτοι η αρμονική ή υπενάντιος και η ενάντιος της υπεναντίου. Συγκεκριμένως, δοθέντων δύο ακεραίων αριθμών α και γ (α>γ), δομούντων την Πλατωνικήν συστοιχίαν ταὐτόν-θάτερον, ήτοι 1:2, κατά την Πυθαγόρειον θεωρίαν περί Μεσοτήτων η αρμονική ή υπενάντιος μεσότης

Εκ των ορισμών των ανωτέρω αναλογιών τα μέρη των και τα μεγέθη των και αι υπεροχαί των είναι «κατ’ ἀριθμόν καί ἰσομετρίαν». Τούτο τονίζεται, διότι εις το πρώτον κλάσμα της αναλογίας συμμετέχουν όχι απλοί αριθμοί, αλλά διαφοραί (=μεγέθη) αριθμών.
Επί τῇ βάσει της Πυθαγορείου ρήσεως «ἁρμονία ἐστί κρᾶσις καί σύνθεσις ἐναντίων» ένθα υπονοείται ότι η αρμονία, ήτοι η διαπασών ή η οκτάβα, δομείται υπό της συνθέσεως δύο εναντιοτήτων. της αρμονικής ή υπεναντίου και της εναντίου της υπεναντίου αναλογιών ή αναλογικοτήτων. Την κράσιν και την σύνθεσιν των δύο αναφερθεισών εναντιοτήτων την γράφω ως 3, 4, 5, 6.

Τοιουτοτρόπως, το διάστημα της αρμονίας (2:1), παρεμβληθεισών των τριών μεσοτήτων, κατέστη πενταμερές 6, 8, 9, 10, 12. Λεπτολογούντες έτι περισσότερον, διαπιστούμεν την ύπαρξιν και πέμπτης αναλογίας, της γεωμετρικής αναλογίας, ήτις εκφράζεται εμπλέγδην κι εναλλάγδην υπό της σχέσεως (9/6 = 12/8).
Μεταξύ των διαδοχικών όρων της αριθμητικής αναλογίας 6, 9, 12 σχηματίζονται τα μουσικά διαστήματα του διατονικού γένους διαπέντε (9/6=3/2) και διατεσσάρων (12/9=4/3), ενώ μεταξύ των διαδοχικών όρων της αρμονικής ή υπεναντίου αναλογίας 6, 8, 12 σχηματίζονται τα μουσικά διαστήματα διατεσσάρων (8/6=4/3) και διαπέντε (12/8=3/2).
Μεταξύ των διαδοχικών όρων της εναντίου της υπεναντίου αναλογίας 6, 10, 12 σχηματίζονται τα μουσικά διαστήματα του χρωματικού γένους μείζων έκτη χρωματική (10/6=5/3) και τρίτη ελάσσων χρωματική (12/10=6/5).
Μεταξύ της αρμονικής (8) και αριθμητικής (9) μεσότητος σχηματίζεται το διάστημα του επογδόου τόνου (9/8) και μεταξύ αριθμητικής (9) και της εναντίου της υπεναντίου μεσότητος (10) σχηματίζεται ο ελάσσων χρωματικός τόνος (10/9).
Ανθυφαιρουμένων των διαστημάτων του διατονικού και του χρωματικού γένους, γεννώνται νέα λίαν ενδιαφέροντα χρωματικά μουσικά διαστήματα, ως είναι φερ’ ειπείν το χρωματικόν ημίτονον (16/15), δια του οποίου ομού οι δύο προαναφερθέντες τόνοι δομούν τετράχορδον (9/8 ∙ 10/9 ∙16/15 = 4/3).
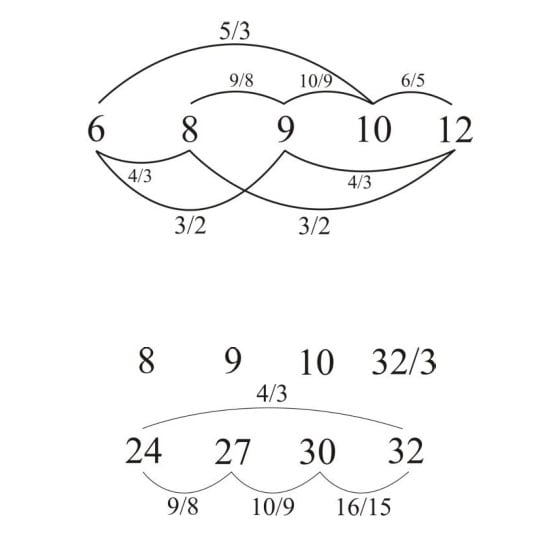
Δια δύο τετραχόρδων καθορίζονται τα μέρη της χρωματικής δομής του διαπασών δια ρητών αριθμών ως ακολούθως:
Το ένα τετράχορδον του διαπασών περιχαρακούται μεταξύ των αριθμών 6 και 8, ήτοι της Νήτης και της Παραμέσης.
Το έτερον τετράχορδον του διαπασών περιχαρακούται μεταξύ των αριθμών 12 και 9, ήτοι της Υπάτης και της Μέσης.
Τα προμνημονευθέντα δύο τετράχορδα είναι διεζευγμένα, οπότε μεταξύ των υπάρχει ο επόγδοος τόνος.
Τοιουτοτρόπως, εδομήθη, ως ο Αριστοτέλης μνημονεύει, το διαπασών διάστημα δια των αδρομερών του διαστηματικών στοιχείων, ήτοι δια των δύο τετραχόρδων του και του επογδόου διαζευκτικού τόνου.
[Συνεχίζεται]

Παρατήρηση: το παρόν άρθρο είναι το τέταρτο μέρος της εισήγησης του Χαράλαμπου Χ. Σπυρίδη, Καθηγητή του Τμήματος Μουσικών Σπουδών Φιλοσοφικής Σχολής Πανεπιστημίου Αθηνών & Κοσμήτορα της Διεθνούς Επιστημονικής Εταιρείας της Αρχαίας Ελληνικής Φιλοσοφίας, με τίτλο «Τέλειον Μεῖζον Σύστημα κατά χρῶμα παρά Πλάτωνι», στην Επιστημονική Ημερίδα «Φιλοσοφία, Φυσικές Επιστήμες, Βιοηθική», που διοργανώθηκε από τη Διεθνή Επιστημονική Εταιρία Αρχαίας Ελληνικής Φιλοσοφίας και την Ένωση Ελλήνων Φυσικών, στο Πανεπιστήμιο Αθηνών, στις 12/11/2014.
Το τρίτο μέρος της ομιλίας μπορείτε να το διαβάσετε εδώ





